Introduction

As we lever MySQL to build database solutions, we might need to build a MySQL recursive query. In an earlier Database Journal article, I showed how to solve an integer parsing problem with SQL Server recursion. This article will show how to solve that same problem with MySQL recursion, highlighting the strong and weak points of this MySQL feature.

Recursion – the basics

As a basic understanding, we can say that recursive software calls itself in a controlled, structured way. According to the classic definition, recursive software needs the below:

• a base case, where the recursive software system reaches a defined solution state
• some way to move the recursive software towards that base case, in a finite number of steps

But in practice, we can add the below to the mix as requirements:

• a software language/development tool that can handle recursion
• hardware, software, and time resources that will support recursion generally, and handle the scope of the specific recursion problem to solve

Recursion has many more considerations, aspects, and fine points, but we have enough information here to proceed. MySQL, combined with readily available modern hardware, covers all these requirements, so we can build a MySQL recursive query. The software samples we’ll see here assume a MySQL 8.0.19 environment.

The problem we’ll solve

The Database Journal article described above shows how we can decompose a positive base-ten integer into its component base-ten multiples of two. These examples show the idea:

999 = 512 + 256 + 128 + 64 +32 + 4 + 2 + 1

= 2⁹ + 2⁸ + 2⁷ + 2⁶ + 2⁵ + 2² + 2¹ + 2⁰

1025 = 1024 + 1

= 2¹⁰ + 2⁰

Starting with a positive base-10 integer, we want to build a comma-delimited list that looks like these:

999 -> (512, 256, 128, 64, 32, 4, 2, 1)

1025 -> (1024, 1)

A base-ten integer n could potentially pack as many as multiple-of-two components.

SELECT FLOOR(LOG(n, 2)) — SQL Server

SELECT FLOOR(LOG(2, n)) — MySQL

We want to build a MySQL recursive query solution. Of course, different integers will return different numbers of components, but the overall idea works. SQL Server 200 and later offers three types of recursion:

• stored procedures
• common table expressions
• functions

The Database Journal article shows how to build SQL Server solutions to the described problem, with all three recursion types. Only stored procedures will work as a MySQL recursive query solution for us here. MySQL does offer recursive common table expressions, but compared to SQL Server CTE’s, they have major limitations and won’t solve this problem. MySQL functions do not handle recursion at all. This article will explore all of these options.

The MySQL recursive stored procedure solution

We’ll see two MySQL stored procedures in this section. They will operate in a MySQL “schema,” or database, called “recursion_database.” First, build the schema itself with this script:

Next, run this statement:

The MySQL website explains that this statement configures the number of times a MySQL stored procedure can recursively call itself in its specific MySQL environment. Next, run this script to build a stored procedure called “SP_parse_integer”:

This screenshot shows the script in the MySQL editor:

This second script builds stored procedure “call_SP_parse_integer”:

This screenshot shows the script in the MySQL editor:

The second stored procedure call_SP_parse_integer depends on the SP_parse_integer stored procedure. Therefore, run the SP_parse_integer script before the call_SP_parse_integer script, in the order shown above, to prevent any dependency problems. Note that these scripts could return warnings. This screenshot shows the result when we run the call_SP_parse_integer build script, for example:

In line 3, the script tried to drop this stored procedure but did not find it. MySQL returned a warning message that we can ignore.

The MySQL recursive query stored procedure engineering

We’ll first focus on SP_parse_integer because the main action happens there. Line 5 declares INOUT parameter PARAM, of data type BIGINT. When a called MySQL stored procedure changes the value of an INOUT parameter, the calling MySQL recursive query stored procedure can see those changes. As a result, an INOUT parameter operates a lot like a C# Ref parameter, a VB.net ByRef parameter, a C++ reference parameter, etc. In all these cases, we pass parameter addresses that operate as pointers to the parameter values. The calling and called procedures, functions, stored procedures, etc. all see the same value in memory, and therefore, they all see every change that happens to those values. In contrast, a value parameter restricts the visibility of its changes to the procedure or function where those changes happen. This block uses a VB.net ByVal parameter to show how a value parameter works:

The Main code block declares variable num and sets it to 5. In the Main block, step 1 calls the procedure DoubleVal, and passes argument num, with its value of 5. The DoubleVal procedure receives the num value as its own local copy of the original num value, found in the Main block. In DoubleVal, step 2 changes that local num value to 10, and then control returns back to the Main block. The Main block never sees that change, but this approach would prevent the SP_parse_integer MySQL recursive query from working. At step 3, it prints the value that it sees for the num – in this case, 5. The Main block and the DoubleVal procedure see two different copies of num because DoubleVal declared the num parameter as a ByVal, or copied, parameter. This block shows the same code sample, except the DoubleVal procedure declared the num parameter as a ByRef parameter:

Step 3 outputs 10 because both the Main block and the DoubleVal procedure operated on the exact same num value in memory. The SP_parse_integer MySQL recursive query will use this technique. DoubleVal declared the num parameter as a ByRef parameter. This way, both the Main block and DoubleVal see the same value in memory, at the same memory location. As a result, when the DoubleVal procedure changed the value of num in step 2, that change became visible to the Main block at step 3. These ideas extend to other development languages and tools, including MySQL. For a MySQL recursive query, an INOUT stored procedure parameter becomes the equivalent of a Visual Basic ByRef parameter. The engineering behind the MySQL stored procedures featured in this article relies on INOUT parameters.

Note that MySQL offers IN parameters, which operate like the Visual Basic ByVal parameters described above. MySQL also offers OUT parameters. A called MySQL stored procedure that “receives” an OUT parameter can’t see the initial, or starting, the value of an OUT parameter that the calling stored procedure sets for that parameter.

Now we can focus on the SP_parse_integer stored procedure as a MySQL recursive query. As seen above, lines 5 and 6 declare both param and parse_string_param as INOUT parameters. The param parameter holds the integer to parse, and parse_string_param will hold the assembled string that the stored procedure will build. Line 10 declares a local BIGINT variable SP_component, which will hold the individual multiple-of-two values that the stored procedure parses out of the param value. This MySQL recursive query returns NULL for param values less than 1 or greater than 1999998, with the IF-block of lines 12 to 14. The ELSEIF block of lines 16 to 19 becomes the recursion base case. When param reaches zero, the stored procedure finished extracting multiple-of-two values from param itself. Line 16 tests for this, and if true, lines 18 and 19 remove the trailing comma and space (, ) from parse_string_param. Then, they add a closing right parenthesis. For this stored procedure, we’ll ignore the edge case when it returns empty parentheses if we call it with a param value of zero (0).

For this MySQL recursive query, the stored procedure main action happens from lines 23 to 26. Line 23 levers the MySQL POWER, FLOOR, and LOG functions to extract the greatest multiple-of-two from the param value. For param = 1025, for example, line 23 returns as the largest multiple-of-two component in 1025.

SP_component = POWER(2.0, FLOOR(LOG(2, param)));
= POWER(2.0, FLOOR(LOG(2, 1025)));
= POWER(2.0, FLOOR(10.001408194392809));
= POWER(2.0, 10);
= 1024

Line 24 concatenates, or adds, the SP_component value to the parse_string_param parameter value, and includes a trailing comma and space. This line casts the extracted parse_string_param value as a string before the string concatenation. Line 25 subtracts SP_component from the param parameter. This subtraction becomes the step that moves the stored procedure closer to the defined base case. Line 26 then recursively calls SP_parse_integer with INOUT parameters param and parse_string_param. The INOUT parameters guarantee that all recursive calls to this MySQL recursive query operate on the same parameter data values. Line 28 closes the if-block, and lines 30 and 31 close the stored procedure itself.

We’ll use the second stored procedure above – call_SP_parse_integer – to call the SP_parse_integer stored procedure. At line 5, call_SP_parse_integer declares n as a bigint IN parameter. This makes sense because the engineering will not need to make changes to the value of n. In a short-hand way, line 16 sets INOUT variable @return_value to an empty string. Note that we did not need to formally declare it because as a user-defined variable for the MySQL recursive query seen here, we’ll only use it for the specific session we’ll need as we run the stored procedure. We can’t initialize it to NULL, because the later MySQL operations that take NULL as a parameter will return NULL values. This would destroy what we want to accomplish here. Line 17 calls to SP_parse_integer passes n and @return_value. SP_parse_integer will make changes to @return_value, and as an INOUT variable, call_SP_parse_integer will see those returned changes. Line 18 SELECTs @return_value as the stored procedure output. This code will test the stored procedure:

This screenshot shows a test of the code:

This code verifies the output:

SELECT (1048576 + 524288 + 262144 + 131072 + 32768 + 1024 + 64 + 32 + 16 + 8 + 4 + 1);

This screenshot verifies the @return_value calculation shown above:

Recursive MySQL engineering – functions and common table expressions

The Database Journal article mentioned earlier explains that SQL Server handles recursive functions, and showed a recursive function solution to the integer parsing problem. We can certainly build the MySQL equivalent of SQL Server functions (stored functions), but the MySQL website states that MySQL stored functions will not support recursion.

Both MySQL and SQL Server offer common table expressions (CTE’s). SQL Shack writer Syed Shanu covered SQL Server CTE’s in the article SQL Server Common Table Expressions (CTE), and MySQL offers a similar CTE feature. We can build a MySQL recursive query as a CTE. For example, this code will build a recursive MySQL factorial CTE stored procedure called recursive_factorial_CTE:

This screenshot shows the code in the MySQL workbench:

We can test the stored procedure with this code:

This screenshot shows a test of the CTE:

We could try to solve the integer parsing problem with a similar MySQL CTE. This code shows development work for a recursive CTE MySQL solution to that problem:

This screenshot shows the code in the MySQL workbench:

We can test this stored procedure with this code:

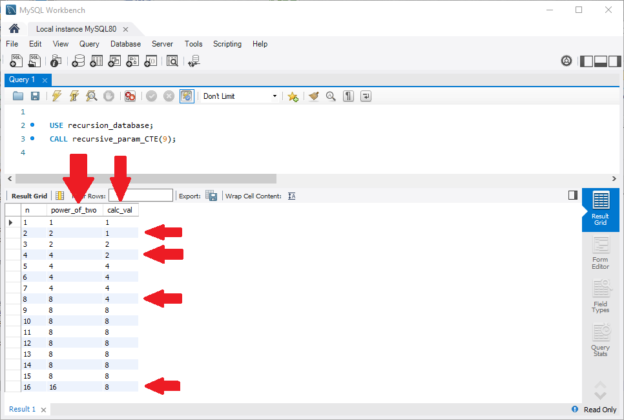
This screenshot shows the output of that test code:

At rows 2, 4, 8, and 16, the values in columns power_of_two and calc_val changed. As the next development step, a filter in the CTE WHERE clause would keep those rows and throw out the other rows. That remaining row set would help as we build the self-contained CTE that we want. At line 19 in the stored procedure, we can see a self‑join in the FROM clause, commented out. A self-join here would make it much easier to filter out the rows we don’t want. Unfortunately, MySQL recursive query CTE’s have a limitation. The MySQL website states that “The recursive SELECT part must reference the CTE only once and only in its FROM clause, not in any subquery.” This means that a recursive MySQL CTE can call itself only one time, and only in its FROM clause. This prevents a self-join in the CTE, which would join the CTE to itself in the CTE code. This self-join technique would make possible a clean, efficient SELECT statement in the CTE. If we restore the full code in line 19 FROM clause, MySQL will return an error when we try to compile the stored procedure, as shown in this screenshot:

The error message at the bottom clearly explains the issue. Ultimately, this restriction prevents a simple recursive MySQL CTE solution to the original problem.

Error Code: 3577. In recursive query block of Recursive Common Table Expression ‘cte’, the recursive table must be referenced only once, and not in any subquery

Conclusion

While we can certainly build recursive MySQL solutions to many database problems, MySQL recursion does not offer the same power and flexibility as that offered by other database products. However, we can expect that MySQL recursive query will match those other products soon enough, as the MySQL product evolves.

• Author
• Recent Posts

Frank Solomon

Frank Solomon started out building Microsoft stack products, and he gradually focused on SQL Server. Some years ago, he began a parallel shift to writing and technical writing. He wrote published articles, he blogs at Bit Vectors, and he co-wrote The SQL Workshop for Packt Publishing, with SQL Shack writer Prashanth Jayaram.

See more about Frank at LinkedIn.
Remove the non-standard characters from this address: fb} <s.author@gmail.com to reach him by email.

Latest posts by Frank Solomon (see all)

• Lever the TSQL MAX/MIN/IIF functions for Pinpoint Row Pivots - May 16, 2022
• Use Kusto Query Language to solve a data problem - July 5, 2021
• Azure Data Explorer and the Kusto Query Language - June 21, 2021