Prediction with Regression in Azure Machine Learning

Introduction

We will be discussing one of the most common prediction technique that is Regression in Azure Machine Learning in this article. After discussing the basic cleaning techniques, feature selection techniques and principal component analysis in previous articles, now we will be looking at a data regression technique in azure machine learning in this article.

Different Types of Regression Techniques

The regression technique is used to forecast by estimating values. There are different regression techniques available in Azure machine learning that supports various data reduction techniques as shown in the following screen.

Let us look at what are the key feature of these techniques of regression in Azure Machine Learning.

Regression Technique	Features
Bayesian Linear Regression	A linear model for small datasets
Boosted Decision Tree Regression	Large memory is required. Fast training time and accurate results.
Decision Forest Regression	Fast training and accurate results.
Fast Forest Quantile Regression	Predict a distribution.
Linear Regression	Linear model and fast training.
Neural Network Regression	Long training time and accurate results.
Ordinal Regression	Data set in rank-ordered categories
Poisson Regression	Predict event counts.

Let us look at the usage of different techniques of regression in azure machine learning in detail.

Linear Regression

One of the most very common techniques in regression is Linear Regression. The linear regression is a linear approach to modelling the relationship between a dependent variable and one or more independent variables. For example, if you want to predict the house prices (dependent variable) by using independent variables of house location, house size, the relationship will be linear.

In the AdventureWorks example, let us say we want to predict the yearly income of customers using other features of customers such as occupation, age, number of children, education, etc.

Let us create an experiment that we have been doing in previous articles as shown in the below screenshot.

Let us rush through the settings in the above experiment as a recap. We have included the AdventureWorks data set that was uploaded before. Since there are a lot of attributes, we have selected only a few columns that will make an impact to decide the yearly income. Those attributes are Marital Status, Gender, Yearly Income, Total Children, Number of Children At Home, Education, Occupation, House Owner, Number of Cars Owned, Age. After the columns are selected, data is split to train and test. In the Train Model, Yearly Income is selected as the predicted column.

We have used linear regression and the following are the configurations of the Linear Regression.

As shown in the above screen, there are two types of methods, Ordinary Least Squares, and Online Gradient Descent methods.

The following are the two parameters for both methods that can be observed from the Train Model control.

Ordinary Least Squares		Online Gradient Descent
Age	6.46262	Age	340.93
Bias	19730	Bias	3732.1
EnglishEducation_Bachelors_0	693.804	EnglishEducation_Bachelors_0	847.45
EnglishEducation_Graduate Degree_1	9802.35	EnglishEducation_Graduate Degree_1	740.45
EnglishEducation_High School_2	-2328.31	EnglishEducation_High School_2	-643.9
EnglishEducation_Partial College_3	8022.83	EnglishEducation_Partial College_3	-80.9
EnglishEducation_Partial High School_4	3539.36	EnglishEducation_Partial High School_4	-622.5
EnglishOccupation_Clerical_0	-16267	EnglishOccupation_Clerical_0	-1881
EnglishOccupation_Management_1	38564	EnglishOccupation_Management_1	2746.6
EnglishOccupation_Manual_2	-29871.3	EnglishOccupation_Manual_2	-2409
EnglishOccupation_Professional_3	22230	EnglishOccupation_Professional_3	2245.3
EnglishOccupation_Skilled Manual_4	5074.31	EnglishOccupation_Skilled Manual_4	-461.4
Gender_F_0	9799.73	Gender_F_0	159.5
Gender_M_1	9930.31	Gender_M_1	81.083
HouseOwnerFlag	-1892.1	HouseOwnerFlag	303.2
MaritalStatus_M_0	9880.4	MaritalStatus_M_0	727.64
MaritalStatus_S_1	9849.63	MaritalStatus_S_1	-487.1
NumberCarsOwned	4218.63	NumberCarsOwned	2081
NumberChildrenAtHome	6711.04	NumberChildrenAtHome	2105.3
TotalChildren	-3314.54	TotalChildren	914.13

You will see that model parameters are different depending on the method that you used in the Liner regression control.

Let us see what is the better method for the above set of data by visualizing the evaluation parameters from the evaluation control.

	Ordinary Least Squares	Online Gradient Descent
Mean Absolute Error	12,950.26	50,614.03
Root Mean Squared Error	17,079.20	58,763.53
Relative Absolute Error	0.51	1.99
Relative Squared Error	0.28	3.35
Coefficient of Determination	0.72	-2.35

By looking at the above comparison, for this dataset, Ordinary Least Squares is better than the Online Gradient Descent as the Ordinary Least Squares has fewer errors and the high coefficient of determination.

Similar to Linear Regression, Bayesian Linear Regression can be used and evaluation is compared as follows.

	Ordinary Least Squares	Online Gradient Descent	Bayesian Linear Regression
Mean Absolute Error	12,950.26	50,614.03	12,949.71
Root Mean Squared Error	17,079.20	58,763.53	17,079.40
Relative Absolute Error	0.51	1.99	0.51
Relative Squared Error	0.28	3.35	0.28
Coefficient of Determination	0.72	-2.35	0.72

Poisson Regression

Poisson regression is used to predict counts. This means Poisson regression prediction will have positive integer numbers. This technique is better suited to predict votes, likes etc.

Let us predict Age of the customer using other parameters. As you know, age cannot be negative and with decimal points. To achieve this, we need to make a few modifications to the above experiment, we need to replace the prediction model with the Poisson regression and change the train model variable to the Age.

The following are the evaluation comparison of Poisson Regression with the Linear regression model.

	Poisson	Linear
Mean Absolute Error	6.76	6.70
Root Mean Squared Error	8.83	8.75
Relative Absolute Error	0.72	0.71
Relative Squared Error	0.60	0.59
Coefficient of Determination	0.40	0.41

You will see from the above table, Poisson regression in Azure machine learning evaluation is similar to the Linear regression. There are parameters available in Poisson regression to enhance the accuracy of the model.

Neural Network Regression

The artificial neural network (ANN) is used in many places in machine learning. In ANN, there are input variables, and there will be a hidden layer from which the output is generated. ANN is mostly used to more complex tasks such as image recognition, character recognition, but it can be used to solve the regression in Azure Machine learning. We will be discussing neural networks in detail in a coming article. In the case of regression, it is just a matter of using the Neural Network regression control and use as a linear regression control.

Boosted Decision Tree and Decision Forest Regression

Decision trees are one of the very common predictive techniques that can be used to classification as well as for regression in Azure Machine Learning. Let us connected the Boosted Decision Tree Regression control in the previously created experiment which was trying to model the prediction of Yearly Income. Let us compare the evaluation parameters of Boosted Decision Tree Regression with the Linear Regression.

	Linear Regression	Boosted Decision Tree
Mean Absolute Error	12,950.26	5,925.07
Root Mean Squared Error	17,079.20	8,897.74
Relative Absolute Error	0.51	0.23
Relative Squared Error	0.28	0.08
Coefficient of Determination	0.72	0.92

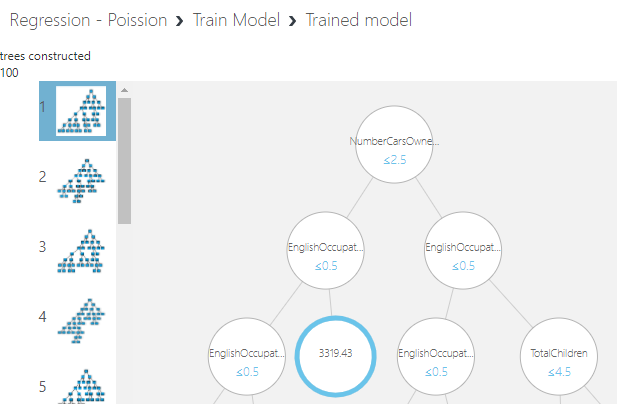
You will see that Decision Forest is much better than the linear regression which is very common even with many datasets. You have the option of looking at the model from the Train Model as shown in the below screenshot.

As configured in the tress model 100 trees are built. You can limit the number of trees to attain higher accuracy. According to this tree, the number of cars is the most important parameter to define the yearly income and next is the Occupation and so on.

Similarly, we can perform regression from Decision Forest Regression and the following are the results for the evaluation parameters.

	Linear Regression	Boosted Decision Tree	Decision Forest
Mean Absolute Error	12,950.26	5,925.07	4143.01
Root Mean Squared Error	17,079.20	8,897.74	8147.90
Relative Absolute Error	0.51	0.23	0.16
Relative Squared Error	0.28	0.08	0.06
Coefficient of Determination	0.72	0.92	0.94

From the above table, you can see that Decision Forest is slightly better than the Boosted Decision tree and it is far better than the Linear Regression in Azure Machine Learning.

Fast Forest Quantile Regression

When predicting a value, practically we want to predict a range rather than an exact value. Fast Forest Quantile Regression in Azure Machine Learning provides a range of prediction rather than an exact value. This control is the same as the other controls, except you can provide the quantities to be estimated as given in the below screenshot.

When predicting using the web service that was discussed in the prediction article, it will predict not only the mean but also the other quantities as shown.

Conclusion

In this article, we looked at different algorithms for Regression in Azure Machine Learning. In azure machine learning, there are rich controls to model regression. We identified that decision tree related regression models are much accurate than other algorithms.

Further References

https://docs.microsoft.com/en-us/azure/machine-learning/studio-module-reference/machine-learning-initialize-model-regression

Introduction to Azure Machine Learning using Azure ML Studio

Data Cleansing in Azure Machine Learning

Prediction in Azure Machine Learning

Feature Selection in Azure Machine Learning

Data Reduction Technique: Principal Component Analysis in Azure Machine Learning

Prediction with Regression in Azure Machine Learning

Prediction with Classification in Azure Machine Learning

Comparing models in Azure Machine Learning

Cross Validation in Azure Machine Learning

Clustering in Azure Machine Learning

Tune Model Hyperparameters for Azure Machine Learning models

Time Series Anomaly Detection in Azure Machine Learning

Designing Recommender Systems in Azure Machine Learning

Language Detection in Azure Machine Learning with basic Text Analytics Techniques

Azure Machine Learning: Named Entity Recognition in Text Analytics

Filter based Feature Selection in Text Analytics

Latent Dirichlet Allocation in Text Analytics

Recommender Systems for Customer Reviews

AutoML in Azure Machine Learning

AutoML in Azure Machine Learning for Regression and Time Series

Building Ensemble Classifiers in Azure Machine Learning

Text Classification in Azure Machine Learning using Word Vectors

Author
Recent Posts

Dinesh Asanka

Dinesh Asanka is MVP for SQL Server Category for last 8 years. He has been working with SQL Server for more than 15 years, written articles and coauthored books. He is a presenter at various user groups and universities. He is always available to learn and share his knowledge.

View all posts by Dinesh Asanka

SQLShack

Prediction with Regression in Azure Machine Learning

Introduction

Different Types of Regression Techniques

Linear Regression

Poisson Regression

Neural Network Regression

Boosted Decision Tree and Decision Forest Regression

Fast Forest Quantile Regression

Conclusion

Further References

Table of contents

Introduction

Different Types of Regression Techniques

Linear Regression

Poisson Regression

Neural Network Regression

Boosted Decision Tree and Decision Forest Regression

Fast Forest Quantile Regression

Conclusion

Further References

Table of contents

Related posts: