First of all, a quick recap on what a recursive query is.

Recursive queries are useful when building hierarchies, traverse datasets and generate arbitrary rowsets etc. The recursive part (simply) means joining a rowset with itself an arbitrary number of times.

A recursive query is defined by an anchor set (the base rowset of the recursion) and a recursive part (the operation that should be done over the previous rowset).

This blogpost will cover some of the basics in recursive CTE’s and explain the approach done by the SQL Server engine.

The basics

A recursive query helps in a lot of scenarios. For instance, where a dataset is built as a parent-child relationship and the requirement is to “unfold” this dataset and show the hierarchy in a ragged format.

A recursive CTE has a defined syntax and can be written in general terms like this …but don’t run way because of the general syntax. A lot of examples (in real code) will come:

Or rewritten in another way:

Another way to write the query (using cross apply):

The last one, with the cross apply, is row based and a lot slower than the other two. It iterates over every row from the previous result and computes the scalar condition (which returns true or false). The same row then gets compared to each row in mytable and the current row of result_from_previous. When these conditions are real – the query can be rewritten as a join. Why you should not use the cross apply for recursive queries.

The reverse – from join to cross apply – is not always true. To know this, we need to look at the algebra of distributivity.

Distributivity algebra

Most of us have already learned that below mathematics is true:

X x (Y + Z) = (X x Y) + (X x Z)

But below is not always true:

X ^ (Y x Z) = (X ^ Z) x (X ^ Y)

Or said with words, distributivity means that the order of operations is not important. The multiplication can be done after the addition and the addition can be done after the multiplication. The result will be the same no matter what.

This arithmetic can be used to generate the relational algebra. It’s pretty straight forward:

set_operation(A union all B, C) = set_operation(A, C) union all set_operation(B, C)

The condition above is true as with the first condition in the arithmetic.

So the union all over the operations is the same as the operations over the union all. This also implies that you cannot use operators like top, distinct, outer join (more exceptions here). The distribution is not the same between top over union all and union all over top. Microsoft has done a lot of good thinking in the recursive approach to reach one ultimate goal – forbid operators that do not distribute over union all.

With this information and knowledge our baseline for building a recursive CTE is now in place.

The first recursive query

Based on the intro and the above algebra we can now begin to build our first recursive CTE.

Consider a sample rowset (sampletree):

From above we can see that Brian refers to Jane who refers to Ditlev. And John refers to Claus. This is fairly easy to read from this rowset – but what if the hierarchy is more complex and unreadable?

A sample requirement could be to “unfold” the hierarchy in a ragged hierarchy so it is directly readable.

The anchor

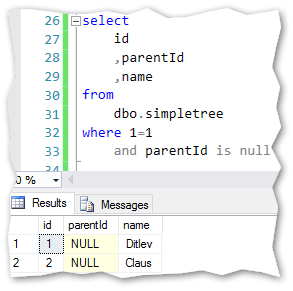
We start with the anchor set (Ditlev and Claus). In this dataset the anchor is defined by parentId is null.

This gives us an anchor-query like below:

Now on to the next part.

The recursive

After the anchor part, we are ready to build the recursive part of the query.

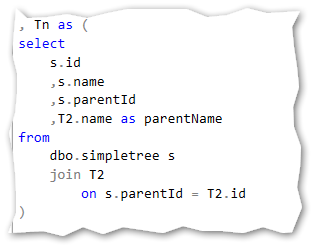
The recursive part is actually the same query with small differences. The main select is the same as the anchor part. We need to make a self join in the select statement for the recursive part.

Before we dive more into the total statement – I’ll show the statement below. Then I’ll run through the details.

Back to the self-reference. Notice the two red underlines in the code. The top one indicates the CTE’s name and the second line indicates the self-reference. This is joined directly in the recursive part in order to do the arithmetic logic in the statement. The join is done between the recursive results parentId and the id in the anchor result. This gives us the possibility to get the name column from the anchor statement.

Notice that I’ve also put in another blank field in the anchor statement and added the parentName field in the recursive statement. This gives us the “human readable” output where I can find the hierarchy directly by reading from left to right.

To get data from the above CTE I just have to make a select statement from this:

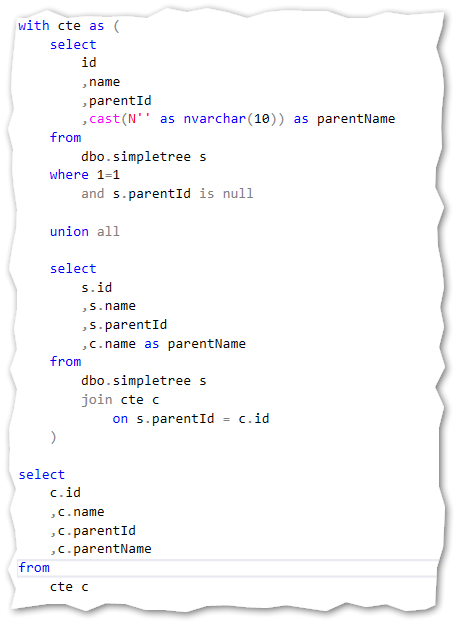
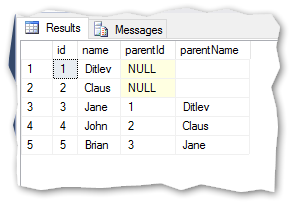
And the results:

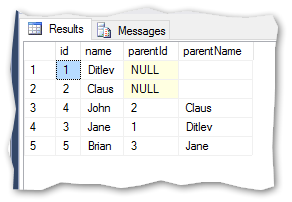
I can now directly read that Jane refers to Ditlev and Brian refers to Jane.

But how is this done when the SQL engine executes the query – the next part tries to explain that.

The SQL engines handling

Given the full CTE statement above I’ll try to explain what the SQL engine does to handle this.

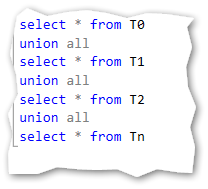
The documented semantics is as follows:

1. Split the CTE into anchor and recursive parts

2. Run the anchor member creating the first base result set (T₀)

3. Run the recursive member with T_i as an input and T_i+1 as an output

4. Repeat step 3 until an empty result set is returned

5. Return the result set. This is a union all set of T₀ to T_n

So let me try to rewrite the above query to match this sequence.

The anchor statement we already know:

First recursive query:

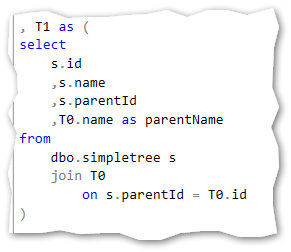
Second recursive query:

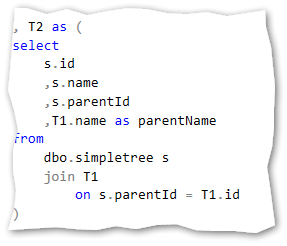
The n recursive query:

The union all statement:

This gives us the exactly same result as we saw before with the rewrite:

Notice that the statement that I’ve put in above named Tn is actually empty. This to give the example of the empty statement that makes the SQL engine stop its execution in the recursive CTE.

This is how I would describe the SQL engines handling of a recursive CTE.

Based on this very simple example, I guess you already can think of ways to use this in your projects and daily tasks.

But what about the performance and execution plan?

Performance

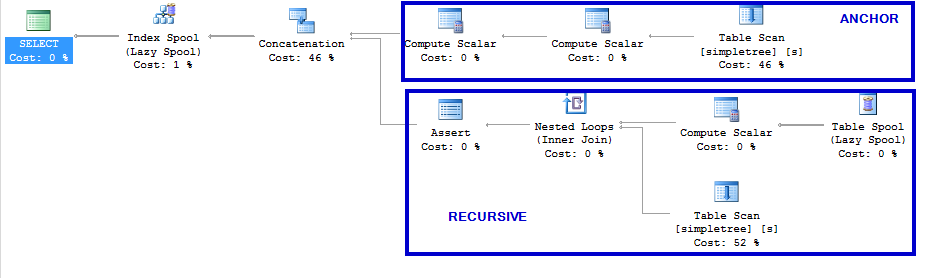
The execution plan for the original recursive CTE looks like this:

The top part of this execution plan is the anchor statement and the bottom part is the recursive statement.

Notice that I haven’t made any indexes in the table, so we are reading on heaps here.

But what if the data is more complex in structure and depth. Let’s try to base the answer on an example:

From the attached sql code you’ll find a script to generate +20.000 rows in a new table called complextree. This data is from a live solution and contains medical procedure names in a hierarchy. The data is used to show the relationships in medical procedures done by the Danish hospital system. It is both deep and complex in structure. (Sorry for the Danish letters in the data…).

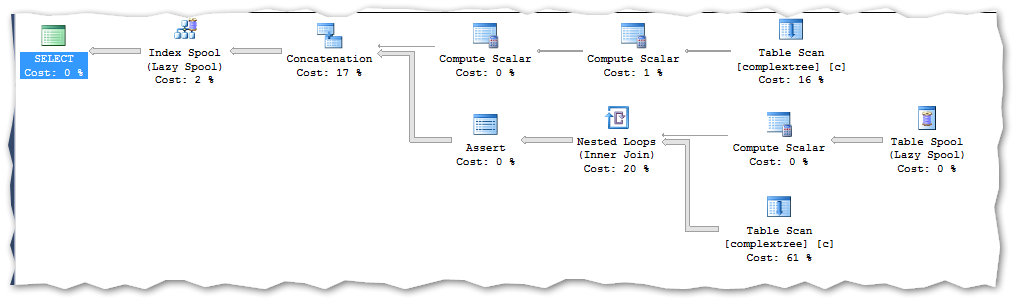
When we run a recursive CTE on this data – we get the exactly same execution plan:

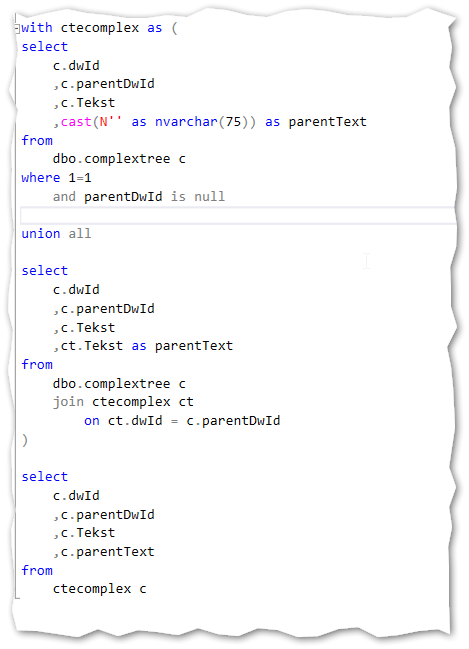
This is also what I would expect as the amount of data when read from heaps very seldom impact on the generated execution plan.

The query runs on my PC for 25 seconds.

Now let me put an index in the table and let’s see the performance and execution plan.

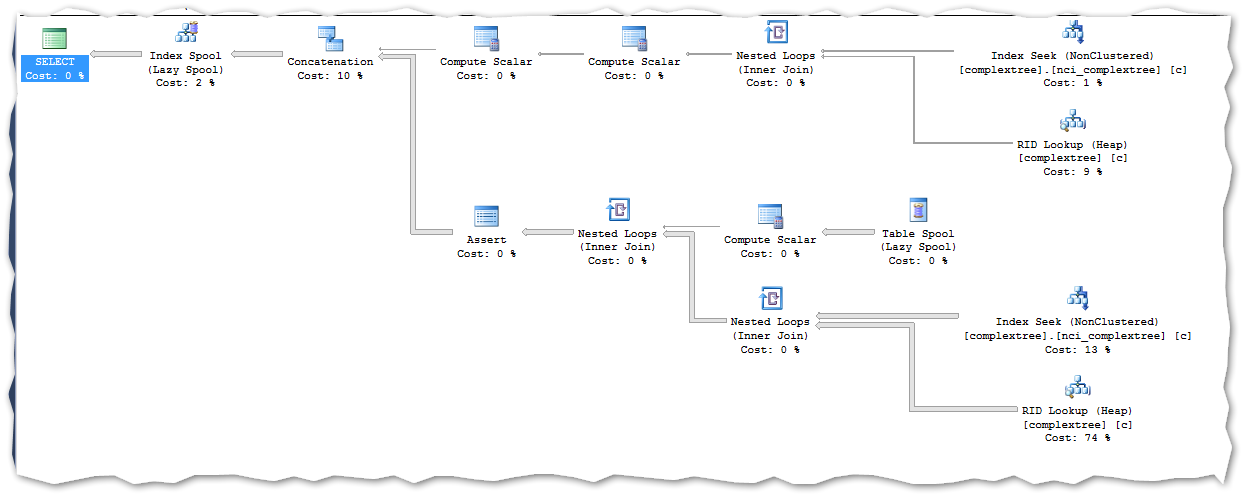
The index is only put on the parentDwId as, according to our knowledge from this article is the recursive parts join column.

The query now runs 1 second to completion and generates this execution plan:

The top line is still the anchor and the bottom part is the recursive part. Notice now the SQL engine uses the non-clustered index to perform the execution and the performance gain is noticeable.

Conclusion

I hope that you’ve now become more familiar with the recursive CTE statement and are willing to try it on your own projects and tasks.

The basics is somewhat straight forward – but beware that the query can become complex and hard to debug as the demand for data and output becomes stronger. But don’t be scared. As I always say – “Don’t do a complex query all at once, start small and build it up as you go along”.

Happy coding.

Complete script can be downloaded here.

• Author
• Recent Posts

Brian Bønk Rueløkke

Brian works as a Business Intelligence and Database architect at Rehfeld – part of IMS Health.

His work spans from the small tasks to the biggest projects. Engaging all the roles from manual developer to architect in his 11 years experience with the Microsoft Business Intelligence stack. With his two certifications MSCE Business Intelligence and MCSE Data Platform, he can play with many cards in the advisory and development of Business Intelligence solutions. The BIML technology has become a bigger part of Brians approach to deliver fast-track BI projects with a higher focus on the business needs.

View all posts by Brian Bønk Rueløkke

Latest posts by Brian Bønk Rueløkke (see all)

• How to import flat files with a varying number of columns in SQL Server - February 22, 2017
• Ready, SET, go – How does SQL Server handle recursive CTE’s - August 19, 2016
• Use of hierarchyid in SQL Server - July 29, 2016